微積分總整理:超高效學習!精準掌握搶分關鍵
活動訊息
內容簡介
喚醒沉睡的數學腦!
與微積分再次相遇
由身為數學補習班權威的作者
滿懷熱情地解說微積分的基本解法技巧並深入探討其中的精髓
微積分被視為高中數學頂點的原因是,
要理解微積分就必須先理解其他各式各樣單元的緣故,
學習微積分,會有原本分散的各個單元逐漸合而為一的感受。
微積分在很大程度上也存在計算技巧的一面,
為了見證微積分計算的真實樣貌本書沒有刻意避開數學式,
且在數式變形的詳細程度幾乎是其他書籍無法比擬的。
同時,也準備了很多激發讀者好奇心的巧思,
其中既有如綠洲般,幫助因數式變形感到疲累的腦袋放鬆的內容,
也有透過數學式探討,將數學作為「語言」來理解的內容。
為了讓各位登上高中數學的頂點,
對於必要的函數、數列還有極限等內容都不會省略,
而且將從原理及原則開始說起,
這也代表我們並不是把山腰當作起點,而是打算從山腳下開始引導各位向前。
只要腳踏實地一步一腳印,一定能到達高中數學的頂端,
雖然很遺憾沒有纜車可以搭乘,但也因為如此,
靠自己的雙腳站在上面時才更加喜悅。
來吧,拿出勇氣踏出第一步!
與微積分再次相遇
由身為數學補習班權威的作者
滿懷熱情地解說微積分的基本解法技巧並深入探討其中的精髓
微積分被視為高中數學頂點的原因是,
要理解微積分就必須先理解其他各式各樣單元的緣故,
學習微積分,會有原本分散的各個單元逐漸合而為一的感受。
微積分在很大程度上也存在計算技巧的一面,
為了見證微積分計算的真實樣貌本書沒有刻意避開數學式,
且在數式變形的詳細程度幾乎是其他書籍無法比擬的。
同時,也準備了很多激發讀者好奇心的巧思,
其中既有如綠洲般,幫助因數式變形感到疲累的腦袋放鬆的內容,
也有透過數學式探討,將數學作為「語言」來理解的內容。
為了讓各位登上高中數學的頂點,
對於必要的函數、數列還有極限等內容都不會省略,
而且將從原理及原則開始說起,
這也代表我們並不是把山腰當作起點,而是打算從山腳下開始引導各位向前。
只要腳踏實地一步一腳印,一定能到達高中數學的頂端,
雖然很遺憾沒有纜車可以搭乘,但也因為如此,
靠自己的雙腳站在上面時才更加喜悅。
來吧,拿出勇氣踏出第一步!
目錄
序言──站上高中數學的頂端吧
第1部 微分之卷
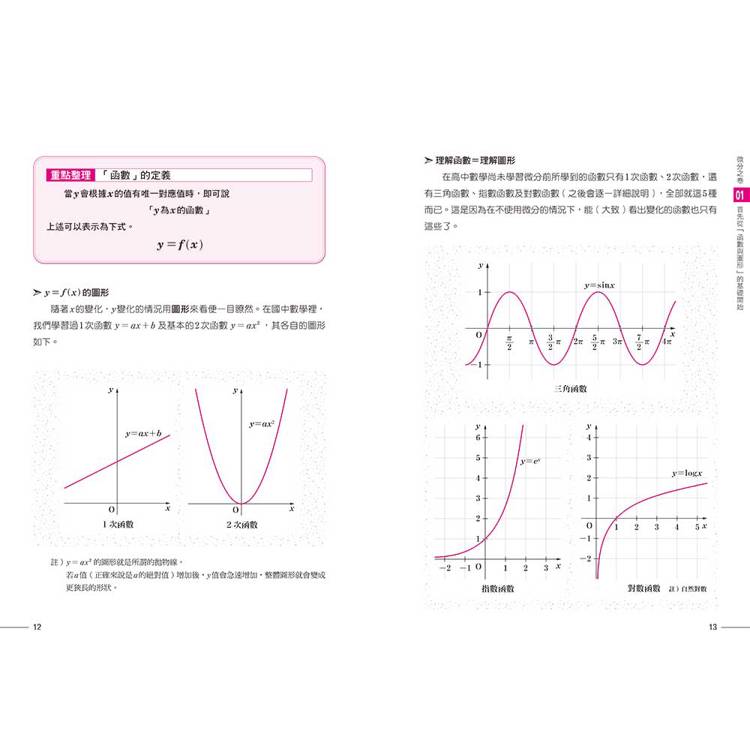
§01 首先從「函數與圖形」的基礎開始
§02 抓住變化的第一步───平均變化率
§03 「等差」數列之和、「等比」數列之和
§04 望向遙遠的彼端───數列的極限
§05 攻略「分母為零」───函數的極限
題外話① 零不能作為除數的原因
§06 「微分係數」指的是切線斜率
§07 物理方面的應用①:瞬間速度
§08 排列、組合與「二項式定理」
§09 自己動手推導微分係數公式!
§10 分析變化───導函數與增減表
§11 外部微分!內部微分!───合成函數的微分
§12 利用數式變形推導───微分的乘法與除法
§13 快速複習①:三角比與三角函數
§14 用扇形來思考───三角函數的微分
題外話② 日本人是否曾經涉足微積分?
§15 快速複習②:乘方與指數函數
§16 快速複習③:對數與對數函數
§17 來微分對數函數及指數函數吧!
§18 應用篇①:函數的最大值與最小值
§19 應用篇②:利用直線近似函數
第2部 積分之卷
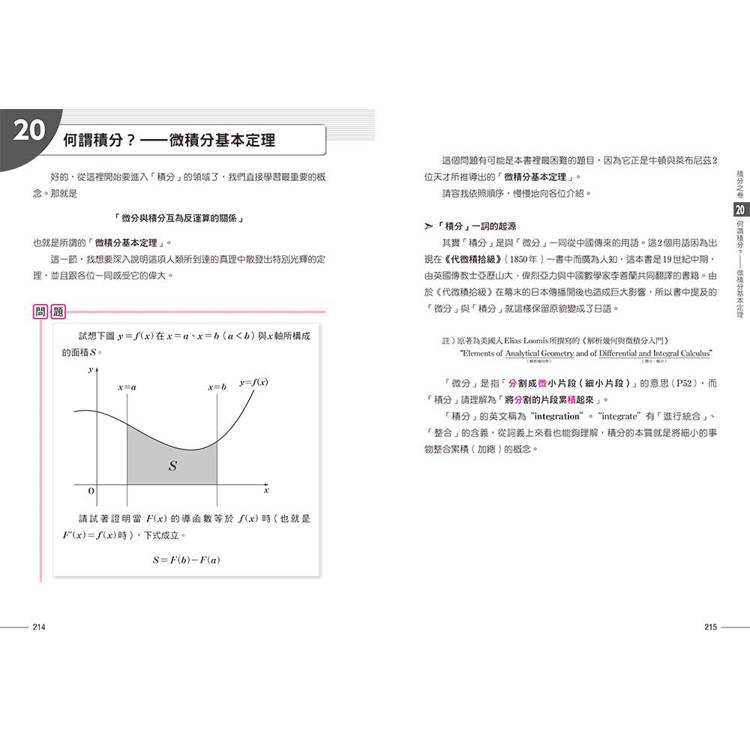
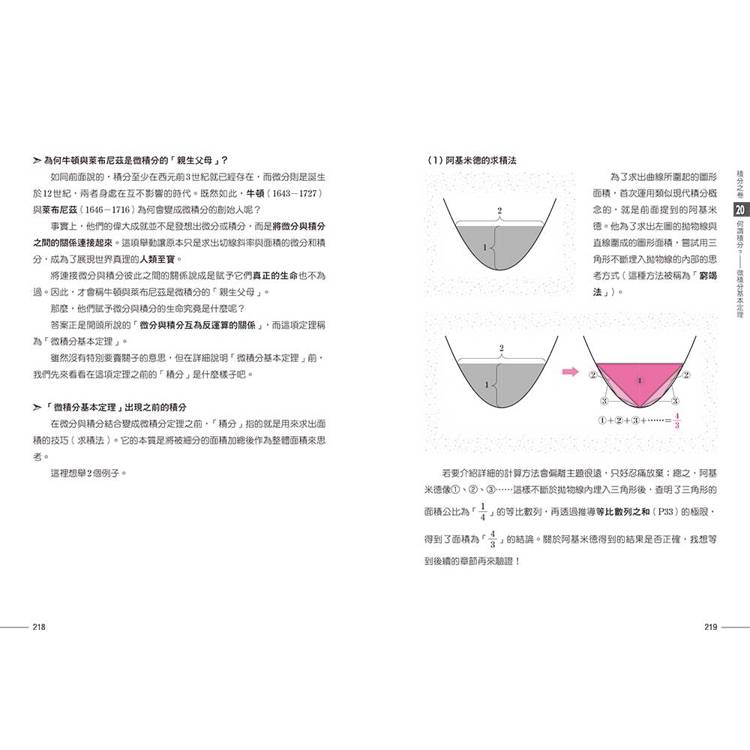
§20 何謂積分?───微積分基本定理
§21 推導不定積分與定積分的公式
§22 積分的技巧───代換積分法
題外話③ 符號之王:萊布尼茲
§23 定積分的應用①:求面積
§24 定積分的應用②:求體積
§25 物理方面的應用②:微分方程式
題外話④ 天氣預報不準的原因
結語──前方道路的景象
第1部 微分之卷
§01 首先從「函數與圖形」的基礎開始
§02 抓住變化的第一步───平均變化率
§03 「等差」數列之和、「等比」數列之和
§04 望向遙遠的彼端───數列的極限
§05 攻略「分母為零」───函數的極限
題外話① 零不能作為除數的原因
§06 「微分係數」指的是切線斜率
§07 物理方面的應用①:瞬間速度
§08 排列、組合與「二項式定理」
§09 自己動手推導微分係數公式!
§10 分析變化───導函數與增減表
§11 外部微分!內部微分!───合成函數的微分
§12 利用數式變形推導───微分的乘法與除法
§13 快速複習①:三角比與三角函數
§14 用扇形來思考───三角函數的微分
題外話② 日本人是否曾經涉足微積分?
§15 快速複習②:乘方與指數函數
§16 快速複習③:對數與對數函數
§17 來微分對數函數及指數函數吧!
§18 應用篇①:函數的最大值與最小值
§19 應用篇②:利用直線近似函數
第2部 積分之卷
§20 何謂積分?───微積分基本定理
§21 推導不定積分與定積分的公式
§22 積分的技巧───代換積分法
題外話③ 符號之王:萊布尼茲
§23 定積分的應用①:求面積
§24 定積分的應用②:求體積
§25 物理方面的應用②:微分方程式
題外話④ 天氣預報不準的原因
結語──前方道路的景象
序/導讀
序言──站上高中數學的頂端吧
知名的霍金博士在著作『時間簡史』(早川書房出版)中提到,出版一般書籍「每增加一條數學式,書的銷量就會減半」。
當然我也非常清楚,世界上很多人有「數學式過敏症」,但本書並沒有刻意迴避數學式,不如說,反而更加積極使用。
為什麼呢?
這是為了讓讀者們充分理解作為高中數學頂端的微積分的意義與價值。
為了能夠〝運用〞微積分
在微積分相關的書籍中,有不少書籍為了顧及「數學式過敏症」的讀者,會盡量不使用數學式來講解概念。這類書籍在內容上花費的心力也時常讓我感到佩服。
但另一方面,每次看到這樣的書籍我也會擔心,
「這樣做有將微積分的魅力傳達給讀者嗎?」(真是多管閒事!)
畢竟,微積分的偉大之處就是要實際使用後才能開始體會,拋開數學式,僅憑圖像來理解概念,還是無法運用微積分吧。
世界聞名的指揮家小澤征爾先生曾經說過,
「將Do、Mi、So和弦的美妙當作知識記在腦袋的人與實際嘗試用鋼琴彈出Do、Mi、So『美麗』的人是截然不同的」
這句話放在微積分也是同樣的道理。
微積分確實在很大程度上存在計算技巧的一面,但那絕不只是些小把戲而已,而是人類為了抵達真理所獲得的寶貴技術,若不實際運用這些技術,是無法真正體會其便利及偉大的。
本書沒有避開數學式的原因是想要讓各位讀者們見證微積分計算的真實樣貌,讓讀者們發出「哇,好厲害!」的驚嘆,或突然頓悟地拍膝蓋說「原來如此!」,我相信這也能成為各位「下次親自嘗試看看」的範例。
徹底填補「空白」的書
話雖如此,如果只是一味列出數學式的話,本書也沒有出版的意義了,相信只要翻閱一下內容就能明白,本書在數式變形的詳細程度幾乎是其他書籍無法比擬的。另外,在數式變形途中會將使用的公式或過去學習到的內容盡可能寫在數學式附近,所以我認為在本書的數式變形裡不會有「搞不清楚在做什麼」的挫敗感。
當然,除了數學式,在文章中也準備了很多激發讀者好奇心的巧思,其中既有如綠洲般,幫助因數式變形感到疲累的腦袋放鬆的內容,也有透過數學式探討,將數學作為「語言」來理解的內容。
雖然很多人都說「微積分是高中數學的頂點」,但其實微積分在高中數學並不是最困難的,要說困難的話,我認為整數、集合還有機率也絲毫不遜色。
微積分被視為高中數學頂點的原因是,要理解微積分就必須先理解其他各式各樣單元的緣故,學習微積分,會有原本分散的各個單元逐漸合而為一的感受,我在高中時期,透過微積分曾多次感概「阿,原來那個單元就是為了此刻才學習的」。
本書為了讓各位登上高中數學的頂點,對於必要的函數(三角函數、指數函數、對數函數)、數列還有極限等內容都不會省略,而且將從原理及原則開始說起,這也代表我們並不是把山腰當作起點,而是打算從山腳下開始引導各位向前。
無論是數式變形、還是作為前置的其他單元,這些被同類書略過的「空白」處都會在本書詳細說明,因此有基礎的讀者們可能會感到內容有些冗長拖沓,除此之外,也會有比我更專業的人指出數學方面不夠嚴謹吧。
這樣也無妨,這本書是為了曾經學過微積分但只留下棘手印象(沒有深入理解),或文科生對「理科的」微積分抱有高度興趣的人所寫的,對他們來說,盡可能去填補那些「空白」會更有幫助,執著於學問的嚴謹性反而會對理解內容造成阻礙,這是從我多年的教學經驗中得到的結論。
對想要登上高中數學頂端的你,本書時而擔任領路人,時而化身成拐杖,而當踏上頂點的那一刻到來,本書的使命就結束了,但並不需要對之後的事感到擔憂,讀完本書後,你應該就具備獨自開始攀登下一座山頂的實力了,也應該可以享受那讓人眼前一亮的優雅數式變形,還有那無懈可擊、堅若磐石的數學嚴謹性吧。請拿出自信來,朝大學通識課的微積分參考書繼續前進吧。
只要腳踏實地一步一腳印,一定能到達高中數學的頂端,雖然很遺憾沒有纜車可以搭乘,但也因為如此,靠自己的雙腳站在上面時才更加喜悅。來吧,拿出勇氣踏出第一步!
知名的霍金博士在著作『時間簡史』(早川書房出版)中提到,出版一般書籍「每增加一條數學式,書的銷量就會減半」。
當然我也非常清楚,世界上很多人有「數學式過敏症」,但本書並沒有刻意迴避數學式,不如說,反而更加積極使用。
為什麼呢?
這是為了讓讀者們充分理解作為高中數學頂端的微積分的意義與價值。
為了能夠〝運用〞微積分
在微積分相關的書籍中,有不少書籍為了顧及「數學式過敏症」的讀者,會盡量不使用數學式來講解概念。這類書籍在內容上花費的心力也時常讓我感到佩服。
但另一方面,每次看到這樣的書籍我也會擔心,
「這樣做有將微積分的魅力傳達給讀者嗎?」(真是多管閒事!)
畢竟,微積分的偉大之處就是要實際使用後才能開始體會,拋開數學式,僅憑圖像來理解概念,還是無法運用微積分吧。
世界聞名的指揮家小澤征爾先生曾經說過,
「將Do、Mi、So和弦的美妙當作知識記在腦袋的人與實際嘗試用鋼琴彈出Do、Mi、So『美麗』的人是截然不同的」
這句話放在微積分也是同樣的道理。
微積分確實在很大程度上存在計算技巧的一面,但那絕不只是些小把戲而已,而是人類為了抵達真理所獲得的寶貴技術,若不實際運用這些技術,是無法真正體會其便利及偉大的。
本書沒有避開數學式的原因是想要讓各位讀者們見證微積分計算的真實樣貌,讓讀者們發出「哇,好厲害!」的驚嘆,或突然頓悟地拍膝蓋說「原來如此!」,我相信這也能成為各位「下次親自嘗試看看」的範例。
徹底填補「空白」的書
話雖如此,如果只是一味列出數學式的話,本書也沒有出版的意義了,相信只要翻閱一下內容就能明白,本書在數式變形的詳細程度幾乎是其他書籍無法比擬的。另外,在數式變形途中會將使用的公式或過去學習到的內容盡可能寫在數學式附近,所以我認為在本書的數式變形裡不會有「搞不清楚在做什麼」的挫敗感。
當然,除了數學式,在文章中也準備了很多激發讀者好奇心的巧思,其中既有如綠洲般,幫助因數式變形感到疲累的腦袋放鬆的內容,也有透過數學式探討,將數學作為「語言」來理解的內容。
雖然很多人都說「微積分是高中數學的頂點」,但其實微積分在高中數學並不是最困難的,要說困難的話,我認為整數、集合還有機率也絲毫不遜色。
微積分被視為高中數學頂點的原因是,要理解微積分就必須先理解其他各式各樣單元的緣故,學習微積分,會有原本分散的各個單元逐漸合而為一的感受,我在高中時期,透過微積分曾多次感概「阿,原來那個單元就是為了此刻才學習的」。
本書為了讓各位登上高中數學的頂點,對於必要的函數(三角函數、指數函數、對數函數)、數列還有極限等內容都不會省略,而且將從原理及原則開始說起,這也代表我們並不是把山腰當作起點,而是打算從山腳下開始引導各位向前。
無論是數式變形、還是作為前置的其他單元,這些被同類書略過的「空白」處都會在本書詳細說明,因此有基礎的讀者們可能會感到內容有些冗長拖沓,除此之外,也會有比我更專業的人指出數學方面不夠嚴謹吧。
這樣也無妨,這本書是為了曾經學過微積分但只留下棘手印象(沒有深入理解),或文科生對「理科的」微積分抱有高度興趣的人所寫的,對他們來說,盡可能去填補那些「空白」會更有幫助,執著於學問的嚴謹性反而會對理解內容造成阻礙,這是從我多年的教學經驗中得到的結論。
對想要登上高中數學頂端的你,本書時而擔任領路人,時而化身成拐杖,而當踏上頂點的那一刻到來,本書的使命就結束了,但並不需要對之後的事感到擔憂,讀完本書後,你應該就具備獨自開始攀登下一座山頂的實力了,也應該可以享受那讓人眼前一亮的優雅數式變形,還有那無懈可擊、堅若磐石的數學嚴謹性吧。請拿出自信來,朝大學通識課的微積分參考書繼續前進吧。
只要腳踏實地一步一腳印,一定能到達高中數學的頂端,雖然很遺憾沒有纜車可以搭乘,但也因為如此,靠自己的雙腳站在上面時才更加喜悅。來吧,拿出勇氣踏出第一步!
配送方式
-
台灣
- 國內宅配:本島、離島
-
到店取貨:
不限金額免運費



-
海外
- 國際快遞:全球
-
港澳店取:


訂購/退換貨須知
退換貨須知:
**提醒您,鑑賞期不等於試用期,退回商品須為全新狀態**
-
依據「消費者保護法」第19條及行政院消費者保護處公告之「通訊交易解除權合理例外情事適用準則」,以下商品購買後,除商品本身有瑕疵外,將不提供7天的猶豫期:
- 易於腐敗、保存期限較短或解約時即將逾期。(如:生鮮食品)
- 依消費者要求所為之客製化給付。(客製化商品)
- 報紙、期刊或雜誌。(含MOOK、外文雜誌)
- 經消費者拆封之影音商品或電腦軟體。
- 非以有形媒介提供之數位內容或一經提供即為完成之線上服務,經消費者事先同意始提供。(如:電子書、電子雜誌、下載版軟體、虛擬商品…等)
- 已拆封之個人衛生用品。(如:內衣褲、刮鬍刀、除毛刀…等)
- 若非上列種類商品,均享有到貨7天的猶豫期(含例假日)。
- 辦理退換貨時,商品(組合商品恕無法接受單獨退貨)必須是您收到商品時的原始狀態(包含商品本體、配件、贈品、保證書、所有附隨資料文件及原廠內外包裝…等),請勿直接使用原廠包裝寄送,或於原廠包裝上黏貼紙張或書寫文字。
- 退回商品若無法回復原狀,將請您負擔回復原狀所需費用,嚴重時將影響您的退貨權益。


















商品評價