A Functorial Model Theory
This book is an introduction to a functorial model theory based on infinitary language categories. The author introduces the properties and foundation of these categories before developing a model theory for functors starting with a countable fragment of an infinitary language. He also presents a new technique for generating generic models with categories by inventing infinite language categories and functorial model theory. In addition, the book covers string models, limit models, and functorial models.
Higher Mathematics for Engineering and Technology
Based on and enriched by the long-term teaching experience of the authors, this volume covers the major themes of mathematics in engineering and technical specialties. The book addresses the elements of linear algebra and analytic geometry, differential calculus of a function of one variable, and elements of higher algebra. On each theme the authors first present short theoretical overviews and then go on to give problems to be solved. The authors provide the solutions to some typical, relatively difficult problems and guidelines for solving them.The authors consider the development of the self-dependent thinking ability of students in the construction of problems and indicate which problems are relatively difficult. The book is geared so that some of the problems presented can be solved in class, and others are meant to be solved independently. An extensive, explanatory solution of at least one typical problem is included, with emphasis on applications, formulas, and rules.This volume is primarily addressed to advanced students of engineering and technical specialties as well as to engineers/technicians and instructors of mathematics.Key features: Presents the theoretical background necessary for solving problems, including definitions, rules, formulas, and theorems on the particular themeProvides an extended solution of at least one problem on every theme and guidelines for solving some difficult problemsSelects problems for independent study as well as those for classroom time, taking into account the similarity of both sets of problemsDifferentiates relatively difficult problems from others for those who want to study mathematics more deeplyProvides answers to the problems within the text rather than at the back of the book, enabling more direct verification of problem solutionsPresents a selection of problems and solutions that are very interesting not only for the students but also for professor-teacher staff
Computation of Generalized Matrix Inverses and Applications
This volume offers a gradual exposition to matrix theory as a subject of linear algebra. It presents both the theoretical results in generalized matrix inverses and the applications. The book is as self-contained as possible, assuming no prior knowledge of matrix theory and linear algebra.The book first addresses the basic definitions and concepts of an arbitrary generalized matrix inverse with special reference to the calculation of {i, j, ..., k} inverse and the Moore-Penrose inverse. Then, the results of LDL* decomposition of the full rank polynomial matrix are introduced, along with numerical examples. Methods for calculating the Moore-Penrose's inverse of rational matrix are presented, which are based on LDL* and QDR decompositions of the matrix. A method for calculating the A(2)T;S inverse using LDL* decomposition using methods is derived as well as the symbolic calculation of A(2)T;S inverses using QDR factorization.The text then offers several ways on how the introduced theoretical concepts can be applied in restoring blurred images and linear regression methods, along with the well-known application in linear systems. The book also explains how the computation of generalized inverses of matrices with constant values is performed. It covers several methods, such as methods based on full-rank factorization, Leverrier-Faddeev method, method of Zhukovski, and variations of the partitioning method.
Mathematics for Engineers and Science Labs Using Maxima
This book is designed to be a vital companion to math textbooks covering the topics of precalculus, calculus, linear algebra, differential equations, and probability and statistics. While these existing textbooks focus mainly on solving mathematic problems using the old paper-and-pencil method, this book teaches how to solve these problems using Maxima open-source software. Maxima is a system for the manipulation of symbolic and numerical expressions, including differentiation, integration, Taylor series, Laplace transforms, ordinary differential equations, systems of linear equations, polynomials, sets, lists, vectors, and matrices. One of the benefits of using Maxima to solve mathematics problems is the immediacy with which it produces answers. Investing in learning Maxima now will pay off in the future, particularly for students and beginning professionals in mathematics, science, and engineering. The volume will help readers to apply nearly all of the Maxima skills discussed here to future courses and research.
Invariance of Modules Under Automorphisms of Their Envelopes and Covers
The theory of invariance of modules under automorphisms of their envelopes and covers has opened up a whole new direction in the study of module theory. It offers a new perspective on generalizations of injective, pure-injective and flat-cotorsion modules beyond relaxing conditions on liftings of homomorphisms. This has set off a flurry of work in the area, with hundreds of papers using the theory appearing in the last decade. This book gives the first unified treatment of the topic. The authors are real experts in the area, having played a major part in the breakthrough of this new theory and its subsequent applications. The first chapter introduces the basics of ring and module theory needed for the following sections, making it self-contained and suitable for graduate students. The authors go on to develop and explain their tools, enabling researchers to employ them, extend and simplify known results in the literature and to solve longstanding problems in module theory, many of which are discussed at the end of the book.
Functional Linear Algebra
Linear algebra is an extremely versatile and useful subject. It rewards those who study it with powerful computational tools, lessons about how mathematical theory is built, examples for later study in other classes, and much more. Functional Linear Algebra is a unique text written to address the need for a one-term linear algebra course where students have taken only calculus. It does not assume students have had a proofs course. The text offers the following approaches: More emphasis is placed on the idea of a linear function, which is used to motivate the study of matrices and their operations. This should seem natural to students after the central role of functions in calculus. Row reduction is moved further back in the semester and vector spaces are moved earlier to avoid an artificial feeling of separation between the computational and theoretical aspects of the course. Chapter 0 offers applications from engineering and the sciences to motivate students by revealing how linear algebra is used. Vector spaces are developed over R, but complex vector spaces are discussed in Appendix A.1. Computational techniques are discussed both by hand and using technology. A brief introduction to Mathematica is provided in Appendix A.2. As readers work through this book, it is important to understand the basic ideas, definitions, and computational skills. Plenty of examples and problems are provided to make sure readers can practice until the material is thoroughly grasped. AuthorDr. Hannah Robbins is an associate professor of mathematics at Roanoke College, Salem, VA. Formerly a commutative algebraist, she now studies applications of linear algebra and assesses teaching practices in calculus. Outside the office, she enjoys hiking and playing bluegrass bass.
STAAR Grade 8 Math Book and Practice Problems [8th Edition Workbook]
Test Prep Books' STAAR Grade 8 Math Book and Practice Problems [8th Edition Workbook] Taking the STAAR Math Grade 8 test? Want to get a good score? Written by Test Prep Books, this comprehensive study guide includes: Quick OverviewTest-Taking StrategiesIntroductionNumerical Representations and RelationshipsComputations and Algebraic RelationshipsGeometry and MeasurementData Analysis and Personal Financial LiteracyPractice QuestionsDetailed Answer Explanations Studying is hard. We know. We want to help. You can ace your test. Each part of the test has a full review. This study guide covers everything likely to be on the STAAR Math Grade 8 test. Lots of practice test questions are included. Miss one and want to know why? There are detailed answer explanations to help you avoid missing the same question a second time. Are you a bad test taker? Use your time wisely with the latest test-taking strategies. Don't settle for just learning what is on the test. Learn how to be successful with that knowledge. Test Prep Books has drilled down the top test-taking tips. This will help you save time and avoid making common mistakes on test day.Get your STAAR Math Grade 8 study guide. It includes review material, practice test questions, and test-taking strategies.It has everything you need for success.
Algebra 4
This book, the fourth book in the four-volume series in algebra, discusses Lie algebra and representation theory in detail. It covers topics such as semisimple Lie algebras, root systems, representation theory of Lie algebra, Chevalley groups and representation theory of Chevalley groups. Numerous motivating illustrations have been presented along with exercises, enabling readers to acquire a good understanding of topics which they can then use to find the exact or most realistic solutions to their problems.
Advances in Lie Superalgebras
1 A. Alldridge, Z. Shaikh: Superbosonisation, Riesz superdistributions, and highest weight modules.- 2 K. Coulembier: Homological algebra for osp(12n).- 3 A. D'Andrea: Finiteness and orbifold vertex operator algebras.- 4 A. De Sole: On classical finite and affine W -algebras.- 5 M. Gorelik, D. Grantcharov: Q-type Lie superalgebras.- 6 C. Hoyt: Weight modules for the Lie superalgebra D(2,1, a).- 7 R. Fioresi, S. Kwok: On SUSY curves.- 8 V. G. Kac, P. Moseneder Frajria, P. Papi: Dirac operators and the Very Strange Formula for Lie superalgebras.- 9 V. Mazorchuk: Parabolic category O for classical Lie superalgebras.- 10 E. Poletaeva: On Kostant's Theorem for Lie superalgebras.- 11 V. Serganova: Classical Lie superalgebras at infinity.- 12 D. Valeri: Classical W-algebras within the theory of Poisson vertex algebras.- 13 J. van Ekeren: Vertex Operator Superalgebras and Odd Trace Functions.- 14 R. Zhang: Serre presentations of Lie superalgebras
Algebras, Rings and Modules, Volume 2
The theory of algebras, rings, and modules is one of the fundamental domains of modern mathematics. General algebra, more specifically non-commutative algebra, is poised for major advances in the twenty-first century (together with and in interaction with combinatorics), just as topology, analysis, and probability experienced in the twentieth century. This is the second volume of Algebras, Rings and Modules: Non-commutative Algebras and Rings by M. Hazewinkel and N. Gubarenis, a continuation stressing the more important recent results on advanced topics of the structural theory of associative algebras, rings and modules.
Theory and Computation of Complex Tensors and Its Applications
Preface.- Introduction.- The pseudo-spectrum theory.- Perturbation theory.- Tensor complementarity problems.- Plane stochastic tensors.- Neural Networks.- US- and U-eigenpairs of complex tensors.- Randomized algorithms.- Bibliography.- Index.
Matrix Inequalities for Iterative Systems
The book reviews inequalities for weighted entry sums of matrix powers. Applications range from mathematics and CS to pure sciences. It unifies and generalizes several results for products and powers of sesquilinear forms derived from powers of Hermitian, positive-semidefinite, as well as nonnegative matrices. It shows that some inequalities are valid only in specific cases. How to translate the Hermitian matrix results into results for alternating powers of general rectangular matrices? Inequalities that compare the powers of the row and column sums to the row and column sums of the matrix powers are refined for nonnegative matrices. Lastly, eigenvalue bounds and derive results for iterated kernels are improved.
Basics of Matrix Algebra for Statistics with R
A Thorough Guide to Elementary Matrix Algebra and Implementation in RBasics of Matrix Algebra for Statistics with R provides a guide to elementary matrix algebra sufficient for undertaking specialized courses, such as multivariate data analysis and linear models. It also covers advanced topics, such as generalized inverses of singular and rectangular matrices and manipulation of partitioned matrices, for those who want to delve deeper into the subject.The book introduces the definition of a matrix and the basic rules of addition, subtraction, multiplication, and inversion. Later topics include determinants, calculation of eigenvectors and eigenvalues, and differentiation of linear and quadratic forms with respect to vectors. The text explores how these concepts arise in statistical techniques, including principal component analysis, canonical correlation analysis, and linear modeling.In addition to the algebraic manipulation of matrices, the book presents numerical examples that illustrate how to perform calculations by hand and using R. Many theoretical and numerical exercises of varying levels of difficulty aid readers in assessing their knowledge of the material. Outline solutions at the back of the book enable readers to verify the techniques required and obtain numerical answers.Avoiding vector spaces and other advanced mathematics, this book shows how to manipulate matrices and perform numerical calculations in R. It prepares readers for higher-level and specialized studies in statistics.
Algebras, Rings and Modules
The theory of algebras, rings, and modules is one of the fundamental domains of modern mathematics. General algebra, more specifically non-commutative algebra, is poised for major advances in the twenty-first century (together with and in interaction with combinatorics), just as topology, analysis, and probability experienced in the twentieth century. This volume is a continuation and an in-depth study, stressing the non-commutative nature of the first two volumes of Algebras, Rings and Modules by M. Hazewinkel, N. Gubareni, and V. V. Kirichenko. It is largely independent of the other volumes. The relevant constructions and results from earlier volumes have been presented in this volume.
Algebraic Computability and Enumeration Models
This book, Algebraic Computability and Enumeration Models: Recursion Theory and Descriptive Complexity, presents new techniques with functorial models to address important areas on pure mathematics and computability theory from the algebraic viewpoint. The reader is first introduced to categories and functorial models, with Kleene algebra examples for languages. Functorial models for Peano arithmetic are described toward important computational complexity areas on a Hilbert program, leading to computability with initial models. Infinite language categories are also introduced to explain descriptive complexity with recursive computability with admissible sets and urelements. Algebraic and categorical realizability is staged on several levels, addressing new computability questions with omitting types realizably. Further applications to computing with ultrafilters on sets and Turing degree computability are examined. Functorial models computability is presented with algebraic trees realizing intuitionistic types of models. New homotopy techniques are applied to Marin Lof types of computations with model categories. Functorial computability, induction, and recursion are examined in view of the above, presenting new computability techniques with monad transformations and projective sets.This informative volume will give readers a complete new feel for models, computability, recursion sets, complexity, and realizability. This book pulls together functorial thoughts, models, computability, sets, recursion, arithmetic hierarchy, filters, with real tree computing areas, presented in a very intuitive manner for university teaching, with exercises for every chapter. The book will also prove valuable for faculty in computer science and mathematics.
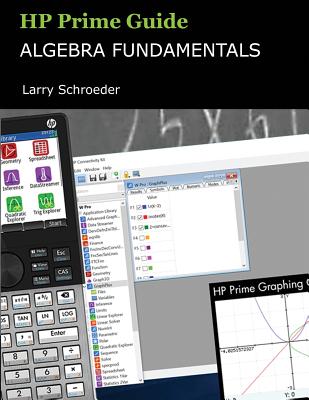
HP Prime Guide Algebra Fundamentals
Welcome to HP Prime Guide Algebra Fundamentals, HP Prime Innovation in Education Series. There is no one road to the learning of mathematics. Different approaches for different learners are needed to take learners to where they want to go. The goal of this guide is to give you the flexibility of various approaches aided by the use of the HP Prime to reach your goals. Manual explanations of math concepts in the guide are accompanied by HP Prime illustrations that can be used with the calculator, computer software, and iOS/ Android/ Windows app. Techniques, examples, and exercises can be done using any of the platforms. The HP Prime Guide Algebra Fundamentals emphasis is its attention on math standards that work. Significant time is spent on learning math by using methods that have shown to be successful in the classroom. There is additional emphasis given to building blocks topics. HP Prime Calculator, HP Prime/Pro, and HP Prime Free Revealed and Extended feature of the guide is used to show how the HP Prime Calculator, HP Prime/Pro, and HP Prime Free commands and functions can be used to work individual problems as well as how they can be extended to help us understand complex math concepts or create a set of tools that can help with problem solving. Upon mastery of the manual techniques apply the HP Prime Calculator, HP Prime/Pro, and HP Prime Free solutions to increase your efficiency and problem solving power. Concentrate on the solution without being bogged down with traditional labor-intense steps. Embrace failure; use your additional time, to attempt more word and real world problems. The HP Prime Guide Algebra Fundamentals is available in print and a digital learning eBook. In the digital eBook version, every example is followed by an interactive reinforcement exercise. Hyperlinks are used to references earlier discussions of a topic, future discussions of a topic, websites, Table of Contents entries, and Detailed Index entries. The hyperlinks are shown as underlined text in the print version. This enables us to see where the eBook's links are. The solutions to the reinforcement exercises are in the back of the printed and eBook versions with eBook's solution linked back to the topic's explanation. In addition to the print version, the guide is available on various eBook readers and eBook applications, be it a stand-alone reader, on a phone, tablet, pc, or through a web-browser. The content in the Guide uses mathematical notation, text, graphics, and HP Prime screenshots. The eBook version takes advantage of the resolution of the display. The real-time access, anytime, anyplace nature of the eBook version, allows a new way for you to gain the math knowledge and skills necessary to succeed in the classroom, at your job, and in your personal pursuit of learning. The print version gives you the option of using a traditional book. An innovative approach is to use HP Prime Calculator, HP Prime/Pro, and HP Prime Free Computer Algebra Solutions (CAS) as an aide in moving forward. In lessons requiring a concept that you have not yet mastered, use the HP Prime Calculator, HP Prime/Pro, and HP Prime Free CAS solutions to assist with class assignments, allowing you to keep current. You keep moving forward with the new material, giving you additional time to master the concept causing problems. Larry Schroeder
Future Vision and Trends on Shapes, Geometry and Algebra
Mathematical algorithms are a fundamental component of Computer Aided Design and Manufacturing (CAD/CAM) systems. This book provides a bridge between algebraic geometry and geometric modelling algorithms, formulated within a computer science framework.Apart from the algebraic geometry topics covered, the entire book is based on the unifying concept of using algebraic techniques - properly specialized to solve geometric problems - to seriously improve accuracy, robustness and efficiency of CAD-systems. It provides new approaches as well as industrial applications to deform surfaces when animating virtual characters, to automatically compare images of handwritten signatures and to improve control of NC machines.This book further introduces a noteworthy representation based on 2D contours, which is essential to model the metal sheet in industrial processes. It additionally reviews applications of numerical algebraic geometry to differential equations systems with multiple solutions and bifurcations.Future Vision and Trends on Shapes, Geometry and Algebra is aimed specialists in the area of mathematics and computer science on the one hand and on the other hand at those who want to become familiar with the practical application of algebraic geometry and geometric modelling such as students, researchers and doctorates.
Common Core Math Grade 7 Study Guide Workbook and Practice Test Questions with Detailed Answer Explanations [7th Edition]
Test Prep Books' Common Core Math Grade 7 Study Guide Workbook and Practice Test Questions with Detailed Answer Explanations [7th Edition]Made by Test Prep Books experts for test takers trying to achieve a great score on the Common Core 7th Grade Math exam.This comprehensive study guide includes: Quick Overview Find out what's inside this guide!Test-Taking Strategies Learn the best tips to help overcome your exam!Introduction Get a thorough breakdown of what the test is and what's on it!Ratios & Proportional Relationships Analyzing Proportional Relationships and Using Them to Solve Real-World ProblemsThe Number System Adding, Subtracting, Multiplying, and Dividing Rational NumbersExpressions & Equations Using Properties of Operations to Generate Equivalent Expressions; Solving Real-Life and Mathematical Problems Using Numerical and Algebraic Expressions and EquationsGeometry Drawing, Constructing, and Describing Geometrical Figures and Describing the Relationships Between Them; Drawing, Constructing, and Describing Geometrical Figures and Describing the Relationships Between ThemStatistics & Probability Using Random Sampling to Draw Inferences About a Population; Drawing Informal Comparative Inferences about Two Populations; Investigating Chance Processes and Developing, Using, and Evaluating Probability ModelPractice Questions Practice makes perfect!Detailed Answer Explanations Figure out where you went wrong and how to improve!Studying can be hard. We get it. That's why we created this guide with these great features and benefits: Comprehensive Review: Each section of the test has a comprehensive review created by Test Prep Books that goes into detail to cover all of the content likely to appear on the test.Practice Test Questions: We want to give you the best practice you can find. That's why the Test Prep Books practice questions are as close as you can get to the actual Common Core 7th Grade Math test.Answer Explanations: Every single problem is followed by an answer explanation. We know it's frustrating to miss a question and not understand why. The answer explanations will help you learn from your mistakes. That way, you can avoid missing it again in the future.Test-Taking Strategies: A test taker has to understand the material that is being covered and be familiar with the latest test taking strategies. These strategies are necessary to properly use the time provided. They also help test takers complete the test without making any errors. Test Prep Books has provided the top test-taking tips.Customer Service: We love taking care of our test takers. We make sure that you interact with a real human being when you email your comments or concerns.Anyone planning to take this exam should take advantage of this Test Prep Books study guide. Purchase it today to receive access to: 7th Grade Common Core Math review materials7th Grade Common Core Math practice test questionsTest-taking strategies
Linear Algebra
LINEAR ALGEBRA EXPLORE A COMPREHENSIVE INTRODUCTORY TEXT IN LINEAR ALGEBRA WITH COMPELLING SUPPLEMENTARY MATERIALS, INCLUDING A COMPANION WEBSITE AND SOLUTIONS MANUALS Linear Algebra delivers a fulsome exploration of the central concepts in linear algebra, including multidimensional spaces, linear transformations, matrices, matrix algebra, determinants, vector spaces, subspaces, linear independence, basis, inner products, and eigenvectors. While the text provides challenging problems that engage readers in the mathematical theory of linear algebra, it is written in an accessible and simple-to-grasp fashion appropriate for junior undergraduate students. An emphasis on logic, set theory, and functions exists throughout the book, and these topics are introduced early to provide students with a foundation from which to attack the rest of the material in the text. Linear Algebra includes accompanying material in the form of a companion website that features solutions manuals for students and instructors. Finally, the concluding chapter in the book includes discussions of advanced topics like generalized eigenvectors, Schur's Lemma, Jordan canonical form, and quadratic forms. Readers will also benefit from the inclusion of: A thorough introduction to logic and set theory, as well as descriptions of functions and linear transformations An exploration of Euclidean spaces and linear transformations between Euclidean spaces, including vectors, vector algebra, orthogonality, the standard matrix, Gauss-Jordan elimination, inverses, and determinants Discussions of abstract vector spaces, including subspaces, linear independence, dimension, and change of basis A treatment on defining geometries on vector spaces, including the Gram-Schmidt process Perfect for undergraduate students taking their first course in the subject matter, Linear Algebra will also earn a place in the libraries of researchers in computer science or statistics seeking an accessible and practical foundation in linear algebra.
Algebra, Geometry and Mathematical Physics
This book collects the proceedings of the Algebra, Geometry and Mathematical Physics Conference, held at the University of Haute Alsace, France, October 2011. Organized in the four areas of algebra, geometry, dynamical symmetries and conservation laws and mathematical physics and applications, the book covers deformation theory and quantization; Hom-algebras and n-ary algebraic structures; Hopf algebra, integrable systems and related math structures; jet theory and Weil bundles; Lie theory and applications; non-commutative and Lie algebra and more.The papers explore the interplay between research in contemporary mathematics and physics concerned with generalizations of the main structures of Lie theory aimed at quantization and discrete and non-commutative extensions of differential calculus and geometry, non-associative structures, actions of groups and semi-groups, non-commutative dynamics, non-commutative geometry and applications in physics and beyond.The book benefits a broad audience of researchers and advanced students.
Spectral Theory of Multivalued Linear Operators
The concept of multivalued linear operators-or linear relations-is the one of the most exciting and influential fields of research in modern mathematics. Applications of this theory can be found in economic theory, noncooperative games, artificial intelligence, medicine, and more. This new book focuses on the theory of linear relations, responding to the lack of resources exclusively dealing with the spectral theory of multivalued linear operators. The subject of this book is the study of linear relations over real or complex Banach spaces. The main purposes are the definitions and characterization of different kinds of spectra and extending the notions of spectra that are considered for the usual one single-valued operator bounded or not bounded. The volume introduces the theory of pseudospectra of multivalued linear operators. The main topics include demicompact linear relations, essential spectra of linear relation, pseudospectra, and essential pseudospectra of linear relations. The volume will be very useful for researchers since it represents not only a collection of a previously heterogeneous material but is also an innovation through several extensions. Beginning graduate students who wish to enter the field of spectral theory of multivalued linear operators will benefit from the material covered, and expert readers will also find sources of inspiration.
The Language Issue in the Teaching of Mathematics in South Africa
Lineare Algebra 1
Im vorliegenden Lehrbuch werden die Grundlagen der Linearen Algebra im Detail vorgestellt: Nachdem die grundlegenden Strukturen der Mathematik - die Gruppen, Ringe und K繹rper - eingef羹hrt sind, werden Vektorr瓣ume und lineare Abbildungen zwischen ihnen ausf羹hrlich vorgestellt. Wichtige Normalformen werden ebenso diskutiert wie die Determinante und das Problem der Diagonalisierung. Abschlie?end werden die Theorien der euklidischen und unit瓣ren Vektorr瓣ume parallel entwickelt.Dieses Buch ist der erste von zwei B瓣nden zur Linearen Algebra. Der Zugang der beiden B瓣nde ist einerseits eher klassisch: die formalen Aspekte der wissenschaftlichen Mathematik werden stark betont. Andererseits wird gerade aus den Anwendungen in der mathematischen Physik wichtige Motivation f羹r das Vorgehen gewonnen. Auf diese Weise ist das Lehrbuch f羹r Studierende der Mathematik und der Physik geeignet. Mehr als 200 umfangreiche ?bungen erleichtern das Selbststudium.
Numerical Linear Algebra and Matrix Factorizations
After reading this book, students should be able to analyze computational problems in linear algebra such as linear systems, least squares- and eigenvalue problems, and to develop their own algorithms for solving them. Since these problems can be large and difficult to handle, much can be gained by understanding and taking advantage of special structures. This in turn requires a good grasp of basic numerical linear algebra and matrix factorizations. Factoring a matrix into a product of simpler matrices is a crucial tool in numerical linear algebra, because it allows us to tackle complex problems by solving a sequence of easier ones. The main characteristics of this book are as follows: It is self-contained, only assuming that readers have completed first-year calculus and an introductory course on linear algebra, and that they have some experience with solving mathematical problems on a computer. The book provides detailed proofs of virtually all results.Further, its respective parts can be used independently, making it suitable for self-study. The book consists of 15 chapters, divided into five thematically oriented parts. The chapters are designed for a one-week-per-chapter, one-semester course. To facilitate self-study, an introductory chapter includes a brief review of linear algebra.
Category Theory and Applications: A Textbook for Beginners (Second Edition)
Category Theory now permeates most of Mathematics, large parts of theoretical Computer Science and parts of theoretical Physics. Its unifying power brings together different branches, and leads to a better understanding of their roots.This book is addressed to students and researchers of these fields and can be used as a text for a first course in Category Theory. It covers the basic tools, like universal properties, limits, adjoint functors and monads. These are presented in a concrete way, starting from examples and exercises taken from elementary Algebra, Lattice Theory and Topology, then developing the theory together with new exercises and applications.A reader should have some elementary knowledge of these three subjects, or at least two of them, in order to be able to follow the main examples, appreciate the unifying power of the categorical approach, and discover the subterranean links brought to light and formalised by this perspective.Applications of Category Theory form a vast and differentiated domain. This book wants to present the basic applications in Algebra and Topology, with a choice of more advanced ones, based on the interests of the author. References are given for applications in many other fields.In this second edition, the book has been entirely reviewed, adding many applications and exercises. All non-obvious exercises have now a solution (or a reference, in the case of an advanced topic); solutions are now collected in the last chapter.
Linear Algebra
There is good reason to be excited about Linear Algebra. With the world becoming increasingly digital, Linear Algebra is gaining more and more importance. When we send texts, share video, do internet searches, there are Linear Algebra algorithms in the background that make it work. This concise introduction to Linear Algebra is authored by a leading researcher presents a book that covers all the requisite material for a first course on the topic in a more practical way. The book focuses on the development of the mathematical theory and presents many applications to assist instructors and students to master the material and apply it to their areas of interest, whether it be to further their studies in mathematics, science, engineering, statistics, economics, or other disciplines. Linear Algebra has very appealing features: -It is a solid axiomatic based mathematical theory that is accessible to a large variety of students.-It has a multitude of applications from many different fields, ranging from traditional science and engineering applications to more 'daily life' applications.-It easily allows for numerical experimentation through the use of a variety of readily available software (both commercial and open source). Several suggestions of different software are made. While MATLAB is certainly still a favorite choice, open-source programs such as Sage (especially among algebraists) and the Python libraries are increasingly popular. This text guides the student to try out different programs by providing specific commands.
Combinatorial Nullstellensatz
Combinatorial Nullstellensatz is a novel theorem in algebra introduced by Noga Alon to tackle combinatorial problems in diverse areas of mathematics. This book focuses on the applications of this theorem to graph colouring. A key step in the applications of Combinatorial Nullstellensatz is to show that the coefficient of a certain monomial in the expansion of a polynomial is nonzero. The major part of the book concentrates on three methods for calculating the coefficients: Alon-Tarsi orientation: The task is to show that a graph has an orientation with given maximum out-degree and for which the number of even Eulerian sub-digraphs is different from the number of odd Eulerian sub-digraphs. In particular, this method is used to show that a graph whose edge set decomposes into a Hamilton cycle and vertex-disjoint triangles is 3-choosable, and that every planar graph has a matching whose deletion results in a 4-choosable graph. Interpolation formula for the coefficient: This method is in particular used to show that toroidal grids of even order are 3-choosable, r-edge colourable r-regular planar graphs are r-edge choosable, and complete graphs of order p+1, where p is a prime, are p-edge choosable. Coefficients as the permanents of matrices: This method is in particular used in the study of the list version of vertex-edge weighting and to show that every graph is (2,3)-choosable. It is suited as a reference book for a graduate course in mathematics.
X Marks the Spot
X Marks the Spot is written from the point of view of the users of mathematics. Since the beginning, mathematical concepts and techniques (such as arithmetic and geometry) were created as tools with a particular purpose like counting sheep and measuring land areas.Understanding those purposes leads to a greater understanding of why mathematics developed as it did. Later mathematical concepts came from a process of abstracting and generalizing earlier mathematics. This process of abstraction is very powerful, but often comes at the price of intuition and understanding. This book strives to give a guided tour of the development of various branches of mathematics (and what they're used for) that will give the reader this intuitive understanding.Features Treats mathematical techniques as tools, and areas of mathematics as the result of abstracting and generalizing earlier mathematical tools Written in a relaxed conversational and occasionally humorous style making it easy to follow even when discussing esoterica. Unravels how mathematicians think, demystifying math and connecting it to the ways non-mathematicians think and connecting math to people's lives Discusses how math education can be improved in order to prevent future generations from being turned off by math.
Linear Algebra
Are you ready to dive into the vibrant world of linear algebra and see how it powers real-world applications? Welcome to this comprehensive guide, where traditional theory meets modern computational practices.Linear algebra is the magic behind many computational sciences -- machine learning, AI, data science, statistics, simulations, computer graphics, multivariate analyses, matrix decompositions, signal processing, and more. But here's a secret: the way it's taught in traditional textbooks isn't how professionals use it in the field.For instance, have you ever wondered about the practical importance of a matrix's "determinant"? You might be in for a surprise! This book bridges the gap between theoretical understanding and practical application, showing you not only the 'what' but also the 'how' of implementing linear algebra in real-world scenarios.What makes this book a must-have resource?Crystal clear explanations of linear algebra concepts and theories.Multiple angles to explain ideas, a proven technique to help cement your understanding.Vivid graphical visualizations to enhance your geometric intuition of linear algebra.Real-world implementations in MATLAB and Python. After all, in today's world, you seldom solve math problems by hand. Software is the way forward!A range of topics from beginner to intermediate levels, including vectors, matrix multiplications, least-squares projections, eigendecomposition, and singular-value decomposition.Emphasis on the application-oriented aspects of linear algebra and matrix analysis.Intuitive visual explanations of diagonalization, eigenvalues and eigenvectors, and singular value decomposition.Ready-to-use codes in MATLAB and Python to bring linear algebra concepts to life on your computer. All codes can be downloaded from https: //github.com/mikexcohen/LinAlgBook.A unique blend of hand-solved exercises and advanced code challenges. Remember, math is not a spectator sport!Whether you're just starting your journey in linear algebra or seeking to apply these concepts to data analyses on computers (such as statistics or signal processing), this book is your go-to guide. With this book at your side, you won't just learn linear algebra; you'll experience it!
Rings, Modules, and Closure Operations
This book presents a systematic exposition of the various applications of closure operations in commutative and noncommutative algebra. In addition to further advancing multiplicative ideal theory, the book opens doors to the various uses of closure operations in the study of rings and modules, with emphasis on commutative rings and ideals. Several examples, counterexamples, and exercises further enrich the discussion and lend additional flexibility to the way in which the book is used, i.e., monograph or textbook for advanced topics courses.
Basic Math Skills Rescue, Part 2
The Critical Foundations of AlgebraThere are three clusters of essential math skills that all students need to learn and master. These are the foundational skills that will gradually lead children to algebra. Students need to have a strong understanding of these topics. These skills are aptly called the Critical Foundations of Algebra.Students need to fully understand these skills conceptually.They need to be able to compute accurately with them.They need to be able to apply them to problem solving.Automatic recall of number facts is also vitally important.The concepts, computation, problem solving, and recall of facts are mutually supportive of one another.The Critical Foundations of AlgebraWhole Numbers.Fractions and decimals, including percents, integers and positive and negative fractions and decimals.Some aspects of measurement and geometry.With a strong background in these areas, students will be prepared for success in algebra and beyond. The importance of a student's success in algebra cannot be over-emphasized. Algebra is the gateway subject that will equip students to take more advanced math, science, and technical classes. Success in algebra opens many doors to a higher education and a rewarding career; lack of success in algebra will sadly result in these doors staying closed.Basic Math Skills Rescue Parts 1 and 2 will ensure mastery of these Critical Skills of Algebra.Part 1 consists of three complete books: Whole numbers & integersFractions DecimalsPart 2 consists of three complete books: GeometryProblem Solving using all the above skillsMore Advanced Pre-Algebra SkillsMath Essentials materials will teach students these vital math skills in the most effective way possible. Here are some of the parent/teacher/student friendly program highlights.Short, concise, non-intimidating, self-contained lessonsA "Helpful Hints" section as part of each lesson, which insures that parents and students alike will understand each new topicFree Access to Online Video Tutorials taught by the authorEach lesson is self-contained and easy to understand with no fluff or distractionsConsistent review is built into each lessonChapter tests and final examsFun and exciting . . . students feel successful and develop self-esteemThe end result . . . Success in Algebra!
Division Workbook Grade 3
Supercharge your child's math skills and help them master division!Do you want to help your child grow into a math whiz? Are you interested in supplementing their learning with a practical book to boost their division skills? Or are you searching for a way to bring them up to speed and help them strengthen weak areas in their learning? Then this book is for you!Designed to be the perfect accompaniment for a school course, curriculum, homework or a tutor, this brilliant 3rd-grade division workbook provides all the essential problems to help children master this crucial area of their math development.A child's early math skills forms the foundation of their long-term math success, so it's never been more important to make sure they're up to speed in this fundamental part of their education. Packed with a wealth of different problems, equations, graphs, exercises and puzzles, this wonderful workbook seeks to be both useful and fun!Book details: - Covers all Areas of 3rd Grade Division- Perfect as a Supplement For Homework, School Curriculum, and For Homeschoolers- Equations Deal With Numbers In The Tens, Hundreds, and Thousands- Includes Equal Divisions, Remainders, Long Division, Word Problems and More- Uses Graphs, Number Lines, and Puzzles To Make Learning Fun!- And Much More!So if you want to strengthen your child's math skills and help them become confident with numbers, then this workbook is for you. Combining challenging questions with engaging exercises, the Division Workbook Grade 3 empowers children to develop their math skills and excel in education!
Problem Based Journey from Elementary Number Theory to an Introduction to Matrix Theory, A: The President Problems
The book is based on lecture notes of a course 'from elementary number theory to an introduction to matrix theory' given at the Technion to gifted high school students. It is problem based, and covers topics in undergraduate mathematics that can be introduced in high school through solving challenging problems. These topics include Number theory, Set Theory, Group Theory, Matrix Theory, and applications to cryptography and search engines.
Associative and Non-Associative Algebras and Applications
Part I: Algebraic and Analytic methods in associative and non-associative structures. Applications.- Behn, A., Casado Y. C. and Molina M. S: Isomorphisms of four dimensional perfect non-simple evolution algebras.- Ouattara, M. and Savadogo, S: Power-associative evolution algebras.- Cabrera-Padilla, M. G., Jim矇nez-Vargas A. and Villegas-Vallecillos, M: A survey on isometries between Lipschitz spaces.- Carmona, J., L籀pez-Mart穩nez, S. and Mart穩nez-Aparicio P. J: The principal eigenvalue for a class of singular quasilinear elliptic operators and applications.- Mart穩n, A. J. C., Dieme, B., and Izquierdo F. J. N: Non-commutative Poisson algebras admitting a multiplicative basis.- Garc穩a, M. C. and Palacios, ? . R: Multiplication algebras: algebraic and analytic aspects.- Oudghiri, M. and Souilah, K: Generalized Drazin inverse and commuting Riesz perturbations.- Louzari, M. and Reyes, A: Generalized rigid modules and their polynomial extensions.- Mart穩n, A. J. C., Gaye, B., and Izquierdo F. J. N: n-Ary k -actions between sets and their applications.- Badry, M. E., Abdallaoui, M. A., and Haily, A: Primary group rings.- Diop, Y., Mesmoudi, L. and Sow, D: Semi-ring based Gr繹bner-Shirshov bases over a noetherian valuation ring.- Haynou, M. and Mohammed Taous, M: The 4-rank of the class group of some real pure quartic number fields.- Part II: Homological and categorical methods in algebra.- Bulacu, D., and Torrecillas, B: Frobenius monoidal algebras and related topics.- Dembele, B., Maaouia M. B. F. and Sanghare, M: The functor SC-1 () and its relationship with homological functors T orn and E XT n.- Kaoutit, L. E.: BOCSES over small linear categories and corings.- Ammar, F., Ayadi, I., Mabrouk, S., and Makhlouf, A: Quadratic color Hom-Lie algebras.- Abdelalim, S., Chaichaa, A. and Garn, M. E: The extension property in the category of direct sum of cyclic torsion-free modules over a BFD.- Part III: History of Mathematics.- Azizi, A.: Arabic Scientific and technical Heritage in Morocco.
Galois Theory and Advanced Linear Algebra
This book discusses major topics in Galois theory and advanced linear algebra, including canonical forms. Divided into four chapters and presenting numerous new theorems, it serves as an easy-to-understand textbook for undergraduate students of advanced linear algebra, and helps students understand other courses, such as Riemannian geometry. The book also discusses key topics including Cayley-Hamilton theorem, Galois groups, Sylvester's law of inertia, Eisenstein criterion, and solvability by radicals. Readers are assumed to have a grasp of elementary properties of groups, rings, fields, and vector spaces, and familiarity with the elementary properties of positive integers, inner product space of finite dimension and linear transformations is beneficial.
Separation in Point-Free Topology
This book is the first systematic treatment of this area so far scattered in a vast number of articles. As in classical topology, concrete problems require restricting the (generalized point-free) spaces by various conditions playing the roles of classical separation axioms. These are typically formulated in the language of points; but in the point-free context one has either suitable translations, parallels, or satisfactory replacements. The interrelations of separation type conditions, their merits, advantages and disadvantages, and consequences are discussed. Highlights of the book include a treatment of the merits and consequences of subfitness, various approaches to the Hausdorff's axiom, and normality type axioms. Global treatment of the separation conditions put them in a new perspective, and, a.o., gave some of them unexpected importance. The text contains a lot of quite recent results; the reader will see the directions the area is taking, and may find inspirationfor her/his further work.The book will be of use for researchers already active in the area, but also for those interested in this growing field (sometimes even penetrating into some parts of theoretical computer science), for graduate and PhD students, and others. For the reader's convenience, the text is supplemented with an Appendix containing necessary background on posets, frames and locales.
Algebra Word Problems Made Simple
NEW from Math Essentials! The perfect companion to the popular No-Nonsense Algebra, Algebra Word Problems Made Simple gives additional help to those who struggle with word problems. Includes a handy glossary and Algebra Resource Center. FREE online video tutorials are available for each chapter.
A School Algebra
This book has been considered by academicians and scholars of great significance and value to literature. This forms a part of the knowledge base for future generations. So that the book is never forgotten we have represented this book in a print format as the same form as it was originally first published. Hence any marks or annotations seen are left intentionally to preserve its true nature.
Graph Path
★ Graph Paper Composition Notebook, 8.5" x 11", 100 Sheets 5X5, Quad Ruled, Large Graph Paper Journal, Grid Paper Notebook, Math and Science Notebook ♥ The graph paper notebook you'll love to use for your projects!Our graph paper composition notebook is a nice book of grid paper. It is great for school, it has good quality and the paper is nice. It is very much like a regular composition book just with grid paper Our grid notebook can be used for drawing, writing, journaling, taking notes at school and so much more. It can be used by kids and adults - students, teachers, artists, architects. ♥ Click buy to get one for your activities and projects. ★ Our graph paper notebook has the following features: Large: 8.5" x 11" 100 Sheets 5X5 High-quality paper and glossy cover for a perfect experience.
Skew Pbw Extensions
This monograph is devoted to a new class of non-commutative rings, skew Poincar矇-Birkhoff-Witt (PBW) extensions. Beginning with the basic definitions and ring-module theoretic/homological properties, it goes on to investigate finitely generated projective modules over skew PBW extensions from a matrix point of view. To make this theory constructive, the theory of Gr繹bner bases of left (right) ideals and modules for bijective skew PBW extensions is developed. For example, syzygies and the Ext and Tor modules over these rings are computed. Finally, applications to some key topics in the noncommutative algebraic geometry of quantum algebras are given, including an investigation of semi-graded Koszul algebras and semi-graded Artin-Schelter regular algebras, and the noncommutative Zariski cancellation problem. The book is addressed to researchers in noncommutative algebra and algebraic geometry as well as to graduate students and advanced undergraduate students.
Affine, Vertex and W-Algebras
This book focuses on recent developments in the theory of vertex algebras, with particular emphasis on affine vertex algebras, affine W-algebras, and W-algebras appearing in physical theories such as logarithmic conformal field theory. It is widely accepted in the mathematical community that the best way to study the representation theory of affine Kac-Moody algebras is by investigating the representation theory of the associated affine vertex and W-algebras. In this volume, this general idea can be seen at work from several points of view. Most relevant state of the art topics are covered, including fusion, relationships with finite dimensional Lie theory, permutation orbifolds, higher Zhu algebras, connections with combinatorics, and mathematical physics. The volume is based on the INdAM Workshop Affine, Vertex and W-algebras, held in Rome from 11 to 15 December 2017. It will be of interest to all researchers in the field.
Ring Theory 2019
Since 1991, the group of ring theorists from China and Japan, joined by Korea from 1995 onwards, took turns to hold the quadrennial international conferences (sometimes also referred to as symposiums). As the proceedings of the eighth conference held in Nagoya, Japan in 2019, this volume consists of a collection of articles by invited speakers (survey) and general speakers (survey and original), all of which were refereed by world experts.The survey articles show the trends of current research and offer clear, thorough explanations that are ideal for researchers also in other specialized areas of ring theory. The original articles display new results, ideas and tools for research investigations in ring theory.The articles cover major areas in ring theory, such as: structures of rings, module theory, homological algebra, groups, Hopf algebras, Lie theory, representation theory of rings, (non-commutative) algebraic geometry, commutative rings (structures, representations), amongst others.This volume is a useful resource for researchers -- both beginners and advanced experts -- in ring theory.
Involutive Category Theory
This monograph introduces involutive categories and involutive operads, featuring applications to the GNS construction and algebraic quantum field theory. The author adopts an accessible approach for readers seeking an overview of involutive category theory, from the basics to cutting-edge applications. Additionally, the author's own recent advances in the area are featured, never having appeared previously in the literature. The opening chapters offer an introduction to basic category theory, ideal for readers new to the area. Chapters three through five feature previously unpublished results on coherence and strictification of involutive categories and involutive monoidal categories, showcasing the author's state-of-the-art research. Chapters on coherence of involutive symmetric monoidal categories, and categorical GNS construction follow. The last chapter covers involutive operads and lays important coherence foundations for applications to algebraic quantum field theory. With detailed explanations and exercises throughout, Involutive Category Theory is suitable for graduate seminars and independent study. Mathematicians and mathematical physicists who use involutive objects will also find this a valuable reference.
Mathematics of Convex and Linear Optimization
Discover the practical impacts of current methods of optimization with this approachable, one-stop resource Linear and Convex Optimization: A Mathematical Approach delivers a concise and unified treatment of optimization with a focus on developing insights in problem structure, modeling, and algorithms. Convex optimization problems are covered in detail because of their many applications and the fast algorithms that have been developed to solve them. Experienced researcher and undergraduate teacher Mike Veatch presents the main algorithms used in linear, integer, and convex optimization in a mathematical style with an emphasis on what makes a class of problems practically solvable and developing insight into algorithms geometrically. Principles of algorithm design and the speed of algorithms are discussed in detail, requiring no background in algorithms. The book offers a breadth of recent applications to demonstrate the many areas in which optimization is successfully and frequently used, while the process of formulating optimization problems is addressed throughout. Linear and Convex Optimization contains a wide variety of features, including: Coverage of current methods in optimization in a style and level that remains appealing and accessible for mathematically trained undergraduates Enhanced insights into a few algorithms, instead of presenting many algorithms in cursory fashion An emphasis on the formulation of large, data-driven optimization problems Inclusion of linear, integer, and convex optimization, covering many practically solvable problems using algorithms that share many of the same concepts Presentation of a broad range of applications to fields like online marketing, disaster response, humanitarian development, public sector planning, health delivery, manufacturing, and supply chain management Ideal for upper level undergraduate mathematics majors with an interest in practical applications of mathematics, this book will also appeal to business, economics, computer science, and operations research majors with at least two years of mathematics training.Software to accompany the text can be found here: https: //www.gordon.edu/michaelveatch/optimization
Elements of Linear and Multilinear Algebra
This set of notes is an activity-oriented introduction to linear and multilinear algebra. The great majority of the most elementary results in these subjects are straightforward and can be verified by the thoughtful student. Indeed, that is the main point of these notes -- to convince the beginner that the subject is accessible. In the material that follows there are numerous indicators that suggest activity on the part of the reader: words such as 'proposition', 'example', 'theorem', 'exercise', and 'corollary', if not followed by a proof (and proofs here are very rare) or a reference to a proof, are invitations to verify the assertions made.These notes are intended to accompany an (academic) year-long course at the advanced undergraduate or beginning graduate level. (With judicious pruning most of the material can be covered in a two-term sequence.) The text is also suitable for a lecture-style class, the instructor proving some of the results while leaving others as exercises for the students.This book has tried to keep the facts about vector spaces and those about inner product spaces separate. Many beginning linear algebra texts conflate the material on these two vastly different subjects.
Lectures in Algebraic Combinatorics
Capturing Adriano Garsia's unique perspective on essential topics in algebraic combinatorics, this book consists of selected, classic notes on a number of topics based on lectures held at the University of California, San Diego over the past few decades. The topics presented share a common theme of describing interesting interplays between algebraic topics such as representation theory and elegant structures which are sometimes thought of as being outside the purview of classical combinatorics. The lectures reflect Garsia's inimitable narrative style and his exceptional expository ability. The preface presents the historical viewpoint as well as Garsia's personal insights into the subject matter. The lectures then start with a clear treatment of Alfred Young's construction of the irreducible representations of the symmetric group, seminormal representations and Morphy elements. This is followed by an elegant application of SL(2) representations to algebraic combinatorics. The last two lectures are on heaps, continued fractions and orthogonal polynomials with applications, and finally there is an exposition on the theory of finite fields. The book is aimed at graduate students and researchers in the field.
Advanced Algebra Study Guide
This book was written to better solve algebra problems using text, graphs, diagrams, rules, combined to show several approaches ofsolving algebra in a real life environment.
Semilocal Categories and Modules with Semilocal Endomorphism Rings
This book collects and coherently presents the research that has been undertaken since the author's previous book Module Theory (1998). In addition to some of the key results since 1995, it also discusses the development of much of the supporting material.In the twenty years following the publication of the Camps-Dicks theorem, the work of Facchini, Herbera, Shamsuddin, Puninski, Prihoda and others has established the study of serial modules and modules with semilocal endomorphism rings as one of the promising directions for module-theoretic research.Providing readers with insights into the directions in which the research in this field is moving, as well as a better understanding of how it interacts with other research areas, the book appeals to undergraduates and graduate students as well as researchers interested in algebra.











![STAAR Grade 8 Math Book and Practice Problems [8th Edition Workbook] STAAR Grade 8 Math Book and Practice Problems [8th Edition Workbook]](https://cdn.kingstone.com.tw/english/images/product/1497/9781637751497m.jpg)









![Common Core Math Grade 7 Study Guide Workbook and Practice Test Questions with Detailed Answer Explanations [7th Edition] Common Core Math Grade 7 Study Guide Workbook and Practice Test Questions with Detailed Answer Explanations [7th Edition]](https://cdn.kingstone.com.tw/english/images/product/5563/9781637755563m.jpg)





























